API Documentation#

The functions described below are part of opyrability and are classified based on their functionality. Each function also contains a worked example based on the famous Shower Problem[11, 13]

Conventional mapping (AIS to AOS)#

Forward mapping#

opyrability.AIS2AOS_map(model: Callable[[...], Union[float, ndarray]], AIS_bound: ndarray, AIS_resolution: ndarray, EDS_bound: ndarray = None, EDS_resolution: ndarray = None, plot: bool = True) → ndarray[source]#

Forward mapping for Process Operability calculations (From AIS to AOS). From an Available Input Set (AIS) bounds and discretization resolution both defined by the user, this function calculates the corresponding discretized Available Output Set (AOS).

This function is part of Python-based Process Operability package.

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Authors: San Dinh & Victor Alves

Parameters:

  • model (Callable[...,Union[float,np.ndarray]]) – Process model that calculates the relationship between inputs (AIS) and Outputs (AOS).

  • AIS_bound (np.ndarray) – Lower and upper bounds for the Available Input Set (AIS).

  • AIS_resolution (np.ndarray) – Resolution for the Available Input Set (AIS). This will be used to discretize the AIS.

  • EDS_bound (np.ndarray) – Lower and upper bounds for the Expected Disturbance Set (EDS). Default is ‘None’.

  • EDS_resolution (np.ndarray) – Resolution for the Expected Disturbance Set (EDS). This will be used to discretize the EDS.

  • plot (bool) – Turn on/off plot. If dimension is d<=3, plot is available and both the Achievable Output Set (AOS) and Available Input Set (AIS) are plotted. Default is True.

Returns:

  • AIS (np.ndarray) – Discretized Available Input Set (AIS).

  • AOS (np.ndarray) – Discretized Available Output Set (AIS).

Example#

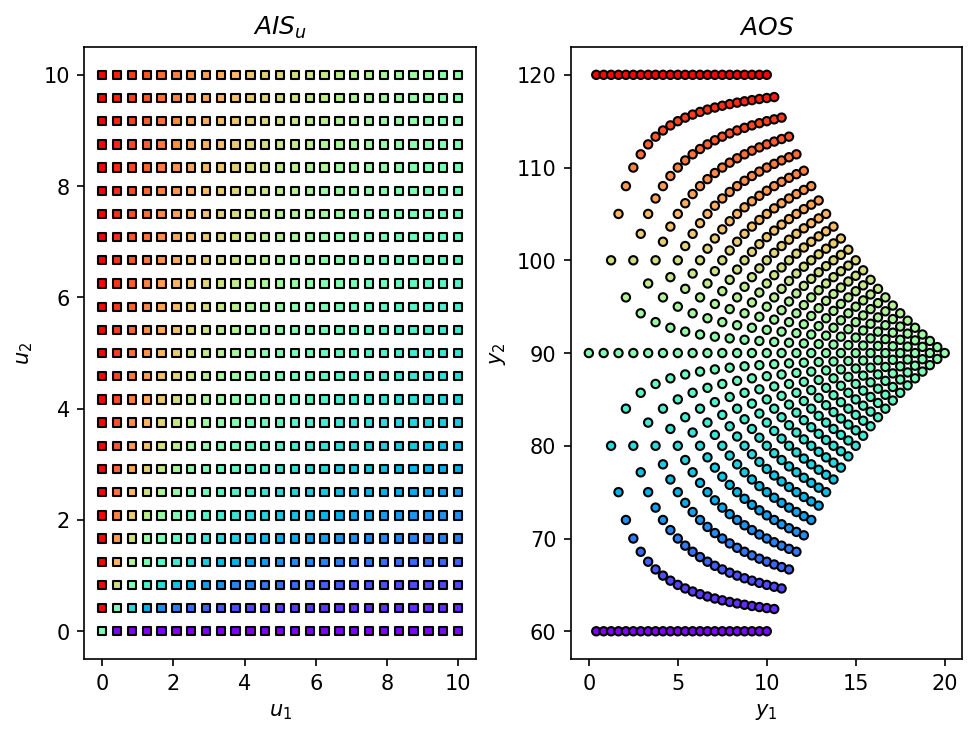
Obtaining the Achievable Output Set (AOS) for the shower problem.

Importing opyrability and Numpy:

    from opyrability import AIS2AOS_map
    import numpy as np

Defining the equations that describe the process:

\[\begin{split}\left\{\begin{array}{c} y_1=u_1+u_2 \\ y_2=\frac{\left(60 u_1+120 u_2\right)}{\left(u_1+u_2\right)} \end{array}\right. \\ \\ y_1 = 0\rightarrow y_2 = 90\end{split}\]
    def shower_problem(u):
        y = np.zeros(2)
        y[0]=u[0]+u[1]
        if y[0]!=0:
            y[1]=(u[0]*60+u[1]*120)/(u[0]+u[1])
        else:
            y[1]=(60+120)/2
            
        return y

Defining the AIS bounds, as well as the discretization resolution:

    AIS_bounds =  np.array([[0, 10], [0, 10]])
    resolution =  [25, 25]

Obtain discretized AIS/AOS.

    AIS, AOS =  AIS2AOS_map(shower_problem, AIS_bounds,  resolution, plot = True)
_images/c00e585754eb2c8f940812f01080d840385b659abd4ca9e061634b818ef0807e.png

Inverse mapping (AOS/DOS to AIS/DIS)#

NLP-Based#

opyrability.nlp_based_approach(model: Callable[[...], Union[float, ndarray]], DOS_bounds: ndarray, DOS_resolution: ndarray, u0: ndarray, lb: ndarray, ub: ndarray, constr=None, method: str = 'ipopt', plot: bool = True, ad: bool = False, warmstart: bool = True) → Union[ndarray, list][source]#

Inverse mapping for Process Operability calculations. From a Desired Output Set (DOS) defined by the user, this function calculates the closest Feasible Desired Ouput set (DOS*) from the AOS and its respective Feasible Desired Input Set (DIS*), which gives insight about potential changes in design and/or operations of a given process model.

This function is part of Python-based Process Operability package.

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Author: Victor Alves

Parameters:

  • model (Callable[...,Union[float,np.ndarray]]) – Process model that calculates the relationship from inputs (AIS-DIS) to outputs (AOS-DOS).

  • DOS_bounds (np.ndarray) – Array containing the bounds of the Desired Output set (DOS). Each row corresponds to the lower and upper bound of each variable.

  • DOS_resolution (np.ndarray) – Array containing the resolution of the discretization grid for the DOS. Each element corresponds to the resolution of each variable. For a resolution defined as k, it will generate d^k points (in which d is the dimensionality of the problem).

  • u0 (np.ndarray) – Initial estimate for the inverse mapping at each point. Should have same dimension as model inputs.

  • lb (np.ndarray) – Lower bound on inputs.

  • ub (np.ndarray) – Upper bound on inputs.

  • constr (list, optional) – List of functions containing constraints to the inverse mapping. The default is None. follows scipy.optimize synthax.

  • method (str) –

    Optimization method used. The default is DE (Differential evolution from scipy). Set ‘ipopt’ if CyIpopt is installed and want to use gradient-based solver. Options are:

    For unconstrained problems:

    -‘trust-constr’

    -‘Nelder-Mead’

    -‘ipopt’

    -‘DE’

    For constrained problems:

    -‘ipopt’

    -‘DE’

    -‘SLSQP’

  • plot (bool) – Turn on/off plot. If dimension is d<=3, plot is available and both the Feasible Desired Output Set (DOS*) and Feasible Desired Input Set (DIS*) are plotted. Default is True.

  • ad (bool) – Turn on/off use of Automatic Differentiation using JAX. If Jax is installed, high-order data (jacobians, hessians) are obtained using AD. Default is False.

Returns:

  • fDIS (np.ndarray) – Feasible Desired Input Set (DIS*). Array containing the solution for each point of the inverse-mapping.

  • fDIS (np.ndarray) – Feasible Desired Output Set (DOS*). Array containing the feasible output for each feasible input calculated via inverse-mapping.

  • message_list (list) – List containing the termination criteria for each optimization run performed for each DOS grid point.

References

[1] J. C. Carrasco and F. V. Lima, “An optimization-based operability framework for process design and intensification of modular natural gas utilization systems,” Comput. & Chem. Eng, 2017. https://doi.org/10.1016/j.compchemeng.2016.12.010

Example#

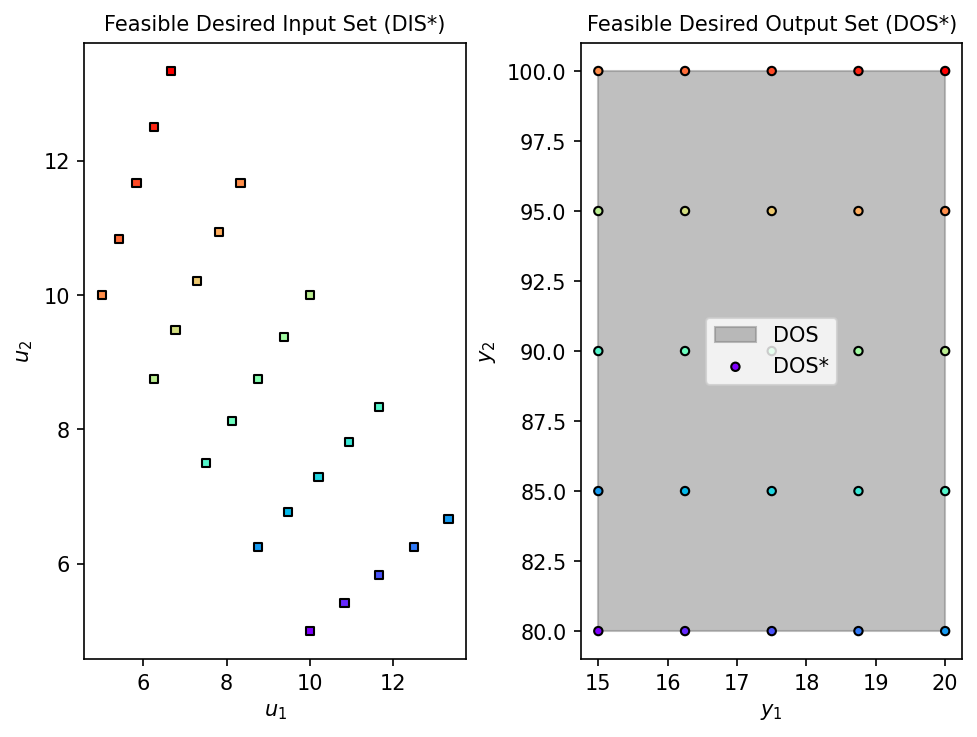
Obtaining the Feasible Desired Input Set (DIS*) for the shower problem.

Importing opyrability and Numpy:

    import numpy as np
    from opyrability import nlp_based_approach

Defining lower and upper bound for the AIS/DIS inverse map:

    lb = np.array([0, 0])
    ub = np.array([100,100])

Defining DOS bounds and resolution to obtain the inverse map:

    DOS_bound = np.array([[15, 20],
                          [80, 100]])
    resolution = [5, 5]

Defining the equations that describe the process:

\[\begin{split}\left\{\begin{array}{c} y_1=u_1+u_2 \\ y_2=\frac{\left(60 u_1+120 u_2\right)}{\left(u_1+u_2\right)} \end{array}\right. \\ \\ y_1 = 0\rightarrow y_2 = 90\end{split}\]
    def shower_problem(u):
        y = np.zeros(2)
        y[0]=u[0]+u[1]
        if y[0]!=0:
            y[1]=(u[0]*60+u[1]*120)/(u[0]+u[1])
        else:
            y[1]=(60+120)/2
            
        return y

Obtaining the DIS*, DOS* and the convergence for each inverse map run. Additionally, using IPOPT as the NLP solver, enabling plotting of the process operability sets, cold-starting the NLP and using finite differences:

    u0 = u0 = np.array([0, 10]) # Initial estimate for inverse mapping.
    fDIS, fDOS, message = nlp_based_approach(shower_problem,
                                             DOS_bound, 
                                             resolution, 
                                             u0, 
                                             lb,
                                             ub, 
                                             method='ipopt', 
                                             plot=True, 
                                             ad=False,
                                             warmstart=False)
_images/1018ba29f9fe1b7d4acbe7168cfb042d75622d9f892e4f721c089f5ded633e83.png

Implicit mapping#

opyrability.implicit_map(model: Callable[[...], Union[float, ndarray]], domain_bound: ndarray, domain_resolution: ndarray, image_init: ndarray, direction: str = 'forward', validation: str = 'predictor-corrector', tol_cor: float = 0.0001, continuation: str = 'Explicit RK4', derivative: str = 'jax', jit: bool = True, step_cutting: bool = False)[source]#

Performs implicit mapping of a implicitly defined process F(u,y) = 0. F can be a vector-valued, multivariable function, which is typically the case for chemical processes studied in Process Operability. This method relies in the implicit function theorem and automatic differentiation in order to obtain the mapping of the required input/output space. The mapping “direction” can be set by changing the ‘direction’ parameter.

Authors: San Dinh & Victor Alves

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Parameters:

  • implicit_model (Callable[...,Union[float,np.ndarray]]) –

    Process model that describes the relationship between the input and output spaces. Has to be written as a function in the following form:

    F(Input Vector, Output Vector) = 0

  • domain_bound (np.ndarray) – Domains of the domain variables. Each row corresponds to the lower and upper bound of each variable. The domain terminology corresponds to the mathematical definition of the domain of a function: If the mapping is in the foward direction (direction = ‘forward’), then the domain corresponds to the process inputs. Otherwise, the mapping is in the inverse direction and the domain corresponds to the process outputs.

  • domain_resolution (np.ndarray) – Array containing the resolution of the discretization grid for the domain. Each element corresponds to the resolution of each variable. For a resolution defined as k, it will generate d^k points (in which d is the dimensionality of the domain).

  • direction (str, optional) – Mapping direction. this will define if a forward or inverse mapping is performed. The default is ‘forward’.

  • validation (str, optional) –

    How the implicit mapping is obatined. The default is ‘predictor-corrector’. The available options are:

    ’predictor’ => Numerical integration only.

    ’corrector’ => Solved using a nonlinear equation solver.

    ’predictor-corrector’ => Numerical integration + correction using nonlinear equation solver if F(u, y) >= Tolerance.

  • tol_cor (float, optional) – Tolerance for solution of the implicit function F(u,y) <= tol_cor. The algorithm will keep solving the implicit mapping while F(u,y) >= tol_cor. The default is 1e-4.

  • continuation (str, optional) –

    Numerical continuation method used in the implicit mapping. The default is ‘Explicit RK4’ .

    ’Explicit Euler’ - Euler’s method. Good for simple (nonstiff) problems.

    ’Explicit RK4’ - Fixed-step 4th order Runge-Kutta. Good for moderate, mildly stiff problems. Good balance between accuracy and complexity.

    ’Odeint’ - Variable step Runge-Kutta. Suitable for challenging, high-dimensional and stiff problems. This is a fully-featured IVP solver.

  • derivative (str, optional) – Derivative calculation method. If JAX is available, automatic differentiation can be performed. The default is ‘jax’.

  • jit (bool True, optional) – JAX’s Just-in-time compilation (JIT) of implicit function and its respective multidimensional derivatives (Jacobians). JIT allows faster computation of the implicit map. The default is ‘True’.

  • step_cutting (bool, False, optional) – Cutting step strategy to subdivide the domain/image in case of stiffness. The default is ‘False’.

Returns:

  • domain_set (np.ndarray) – Set of values that corresponds to the domain of the implicit function.

  • image_set (np.ndarray) – Set of values that corresponds to the calculated image of the implicit function.,

  • domain_polyhedra (list) – Set of coordinates for polytopic construction of the domain. Can be used to create polytopes for multimodel representation and/or OI evaluation (see multimodel_rep and oi_calc modules)

  • image_polyhedra (list) – Set of coordinates for polytopic construction of the calculated image of the implicit function. Similarly to ‘domain_polyhedra’, this list can be used to construct polytopes for multimodel representation and OI evaluation.

References

V. Alves, J. R. Kitchin, and F. V. Lima. “An inverse mapping approach for process systems engineering using automatic differentiation and the implicit function theorem”. AIChE Journal, 2023. https://doi.org/10.1002/aic.18119

Multimodel representation#

opyrability.multimodel_rep(model: Callable[[...], Union[float, ndarray]], bounds: ndarray, resolution: ndarray, polytopic_trace: str = 'simplices', perspective: str = 'outputs', plot: str = True, EDS_bound: str = None, EDS_resolution: str = None)[source]#

Obtain a multimodel representation based on polytopes of Process Operability sets. This procedure is essential for evaluating the Operability Index (OI).

This function is part of Python-based Process Operability package.

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Author: Victor Alves

Parameters:

  • model (Callable[...,Union[float,np.ndarray]]) – Process model that calculates the relationship between inputs (AIS-DIS) and Outputs (AOS-DOS).

  • bounds (np.ndarray) – Bounds on the Available Input Set (AIS), or Desired Output Set (DOS) if an inverse mapping is chosen. Each row corresponds to the lower and upper bound of each AIS or DOS variable.

  • resolution (np.ndarray) – Array containing the resolution of the discretization grid for the AIS or DOS.Each element corresponds to the resolution of each variable. For a resolution defined as k, it will generate d^k points (in which d is the dimensionality of the AIS or DOS).

  • polytopic_trace (str, Optional.) – Determines if the polytopes will be constructed using simplices or polyhedrons. Default is ‘simplices’. Additional option is ‘polyhedra’.

  • perspective (str, Optional.) – Defines if the calculation is to be done from the inputs/outputs perspective. Affects only labels in plots. Default is ‘outputs’.

  • plot (str, Optional.) – Defines if the plot of operability sets is desired (If the dimension is <= 3). Default is ‘True’.

  • EDS_bound (np.ndarray) – Lower and upper bounds for the Expected Disturbance Set (EDS). Default is ‘None’.

  • EDS_resolution (np.ndarray) – Resolution for the Expected Disturbance Set (EDS). This will be used to discretize the EDS, similar to the AIS_resolution

Returns:

mapped_region – List with first argument being a convex polytope or collection of convex polytopes (named as Region) that describes the AOS. Can be used to calculate the Operability Index using OI_eval. Second argument is the coordinates of the AOS as a numpy array.

Return type:

list

References

[1] D. R., Vinson and C. Georgakis. New Measure of Process Output Controllability. J. Process Control, 2000. https://doi.org/10.1016/S0959-1524(99)00045-1

[2] C. Georgakis, D. Uztürk, S. Subramanian, and D. R. Vinson. On the Operability of Continuous Processes. Control Eng. Pract., 2003. https://doi.org/10.1016/S0967-0661(02)00217-4

[3] V.Gazzaneo, J. C. Carrasco, D. R. Vinson, and F. V. Lima. Process Operability Algorithms: Past, Present, and Future Developments. Ind. & Eng. Chem. Res. 59 (6), 2457-2470, 2020. https://doi.org/10.1021/acs.iecr.9b05181

Example#

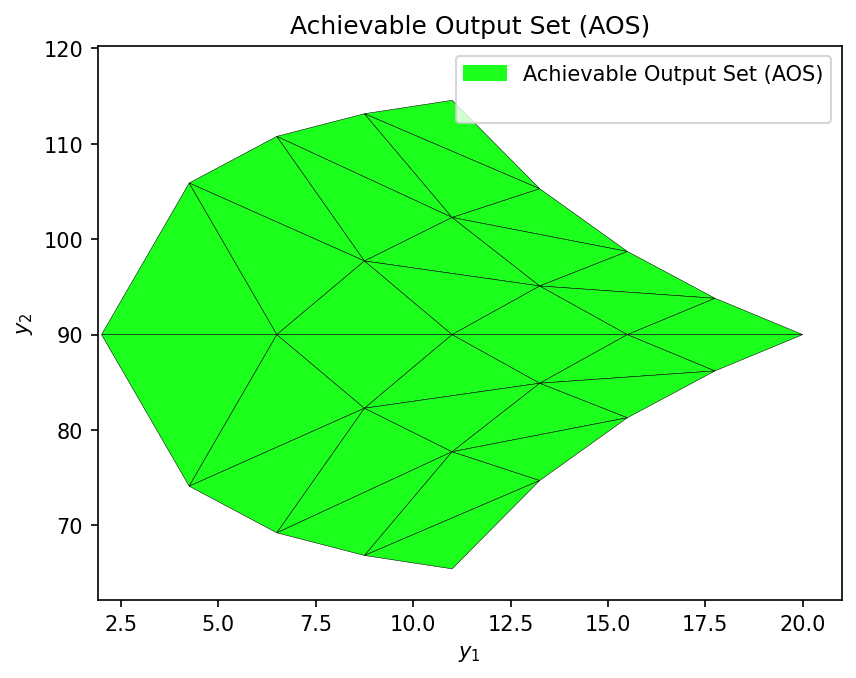
Obtaining the Achievable Output Set (AOS) for the shower problem.

Importing opyrability and Numpy:

    from opyrability import multimodel_rep
    import numpy as np

Defining the equations that describe the process:

\[\begin{split}\left\{\begin{array}{c} y_1=u_1+u_2 \\ y_2=\frac{\left(60 u_1+120 u_2\right)}{\left(u_1+u_2\right)} \end{array}\right. \\ \\ y_1 = 0\rightarrow y_2 = 90\end{split}\]
    def shower_problem(u):
        y = np.zeros(2)
        y[0]=u[0]+u[1]
        if y[0]!=0:
            y[1]=(u[0]*60+u[1]*120)/(u[0]+u[1])
        else:
            y[1]=(60+120)/2
            
        return y

Defining the AIS bounds and the discretization resolution:

    AIS_bounds =  np.array([[1, 10], [1, 10]])
    AIS_resolution =  [5, 5]

Obtaining multimodel representation of paired polytopes for the AOS:

    AOS_region  =  multimodel_rep(shower_problem, AIS_bounds, AIS_resolution)
_images/e52b34d126a092d31ac436ebabdca6ed3a8b1b094cbce19021e4dc9663b68846.png

OI evaluation#

opyrability.OI_eval(AS: Region, DS: ndarray, perspective='outputs', hypervol_calc: str = 'robust', plot: str = True)[source]#

Operability Index (OI) calculation. From a Desired Output Set (DOS) defined by the user, this function calculates the intersection between achievable (AOS) and desired output operation (DOS). Similarly, the OI can be also calculated from the inputs’ perspective, as an intersection between desired input (DIS) and available input (AIS). This function is able to evaluate the OI in any dimension, ranging from 1-d (length) up to higher dimensions (Hypervolumes, > 3-d), aided by the Polytope package.

This function is part of Python-based Process Operability package.

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Author: Victor Alves

Parameters:

  • AS (pc.Region) – Available input set (AIS) or Achievable output set (AOS) represented as a series of paired (and convex) polytopes. This region is easily obtained using the multimodel_rep function.

  • DS (np.ndarray) – Array containing the desired operation, either in the inputs (DIS) or outputs perspective (DOS).

  • perspective (str, Optional.) – String that determines in which perspective the OI will be evaluated: inputs or outputs. default is ‘outputs’.

  • hypervol_calc (str, Optional.) – Determines how the approach when evaluating hypervolumes. Default is ‘robust’, an implementation that switches from qhull’s hypervolume evaluation or polytope’s evaluation depending on the dimensionality of the problem. Additional option is ‘polytope’, Polytope’s package own implementation of hypervolumes evaluation being used in problems of any dimension.

Returns:

OI – Operability Index value. Ranges from 0 to 100%. A fully operable process has OI = 100% and if not fully operable, OI < 100%.

Return type:

float

References

[1] D. R., Vinson and C. Georgakis. New Measure of Process Output Controllability. J. Process Control, 2000. https://doi.org/10.1016/S0959-1524(99)00045-1

[2] C. Georgakis, D. Uztürk, S. Subramanian, and D. R. Vinson. On the Operability of Continuous Processes. Control Eng. Pract., 2003. https://doi.org/10.1016/S0967-0661(02)00217-4

[3] V.Gazzaneo, J. C. Carrasco, D. R. Vinson, and F. V. Lima. Process Operability Algorithms: Past, Present, and Future Developments. Ind. & Eng. Chem. Res. 59 (6), 2457-2470, 2020. https://doi.org/10.1021/acs.iecr.9b05181

Example#

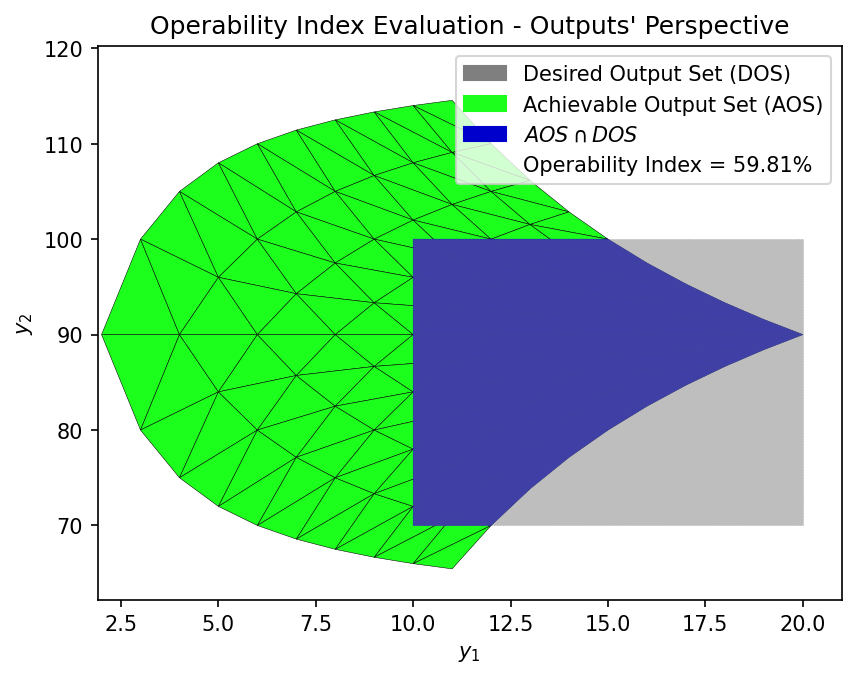
Evaluating the OI for the shower problem for a given DOS.

Importing opyrability and Numpy:

    from opyrability import multimodel_rep, OI_eval
    import numpy as np

Defining the equations that describe the process:

\[\begin{split}\left\{\begin{array}{c} y_1=u_1+u_2 \\ y_2=\frac{\left(60 u_1+120 u_2\right)}{\left(u_1+u_2\right)} \end{array}\right. \\ \\ y_1 = 0\rightarrow y_2 = 90\end{split}\]
    def shower_problem(u):
        y = np.zeros(2)
        y[0]=u[0]+u[1]
        if y[0]!=0:
            y[1]=(u[0]*60+u[1]*120)/(u[0]+u[1])
        else:
            y[1]=(60+120)/2
            
        return y

Defining the AIS bounds and the discretization resolution:

    AIS_bounds =  np.array([[1, 10], [1, 10]])
    AIS_resolution =  [10, 10]

Obtaining multimodel representation of paired polytopes for the AOS:

    AOS_region  =  multimodel_rep(shower_problem, AIS_bounds, AIS_resolution,
    plot=False)

Either plot is not possible (dimension > 3) or you have chosen plot=False. The operability set is still returned as a polytopic region of general dimension.

Defining a DOS region between \(y_1 =[10-20], y_2=[70-100]\)

    DOS_bounds =  np.array([[10, 20], 
                            [70, 100]])

Evaluating the OI and seeing the intersection between the operability sets:

    OI = OI_eval(AOS_region, DOS_bounds)
_images/8047215247b4f4759c5633452f642b55ce2b43fa4bd7f08d8c71c1f326bbcdc6.png

Utilities#

opyrability.create_grid(region_bounds: ndarray, region_resolution: tuple)[source]#

Create a multidimensional, discretized grid, given the bounds and the resolution.

This function is part of Python-based Process Operability package.

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Author: San Dinh

Parameters:

  • region_bounds (np.ndarray) – Numpy array that contains the bounds of a (possibily) multidimensional region. Each row corresponds to the lower and upper bound of each variable that constitutes the hypercube.

  • region_resolution (np.ndarray) – Array containing the resolution of the discretization grid for the region. Each element corresponds to the resolution of each variable. For a resolution defined as k, it will generate d^k points (in which d is the dimensionality of the problem).

Returns:

region_grid – Multidimensional array that represents the grid descritization of the region in Euclidean coordinates.

Return type:

np.ndarray

Example#

Creating a 2-dimensional discretized rectangular grid for given DOS bounds.

    from opyrability import create_grid

    DOS_bounds =  np.array([[10, 20], 
                            [70, 100]])

    DOS_resolution =  [3, 3]

    DOS_points = create_grid(DOS_bounds, DOS_resolution)

    print(DOS_points)

[[[ 10.  70.]
  [ 10.  85.]
  [ 10. 100.]]

 [[ 15.  70.]
  [ 15.  85.]
  [ 15. 100.]]

 [[ 20.  70.]
  [ 20.  85.]
  [ 20. 100.]]]

Visualizing this grid:

    import matplotlib.pyplot as plt

    DOS_points = DOS_points.reshape(-1, 2)

    plt.scatter(DOS_points[:, 0], DOS_points[:, 1])

<matplotlib.collections.PathCollection at 0x2610239ca10>
_images/f875edd32bca6c939cdff4cdcab8cc7cb644ca8b163436dab176f5adbb7edcc1.png
opyrability.points2simplices(AIS: ndarray, AOS: ndarray) → ndarray[source]#

Generation of connected simplices (k+1 convex hull of k+1 vertices) based on the AIS/AOS points.

This function is part of Python-based Process Operability package.

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Author: San Dinh

Parameters:

  • AIS (np.ndarray) – Array containing the points that constitutes the AIS.

  • AOS (np.ndarray) – Array containing the points that constitutes the AOS.

Returns:

  • AIS_simplices (np.ndarray) – List of input (AIS) vertices for each simplex generated, in the form of an array.

  • AOS_simplices (np.ndarray) – List of output (AOS) vertices for each simplex generated, in the form of an array.

Example#

Generating paired simplicial polytopes for the AIS/AOS generated for the shower problem example.

    from opyrability import AIS2AOS_map
    from opyrability import points2simplices

    # Obtain an input-output mapping using AIS2AOS_map
    AIS_bounds =  np.array([[0, 10], [0, 10]])
    resolution =  [5, 5]

    # The shower_problem function is the same one from the AIS2AOS_map example.
    AIS, AOS =  AIS2AOS_map(shower_problem, AIS_bounds,  resolution, plot = False)
    
    # Obtain simplices.
    AIS_poly, AOS_poly = points2simplices(AIS,AOS)

    print('AIS Simplices \n', AIS_poly)
    print('AOS Simplices \n', AOS_poly)

AIS Simplices 
 [array([[0. , 0. ],
       [0. , 2.5],
       [2.5, 2.5]]), array([[0. , 0. ],
       [2.5, 0. ],
       [2.5, 2.5]]), array([[2.5, 0. ],
       [2.5, 2.5],
       [5. , 2.5]]), array([[2.5, 0. ],
       [5. , 0. ],
       [5. , 2.5]]), array([[5. , 0. ],
       [5. , 2.5],
       [7.5, 2.5]]), array([[5. , 0. ],
       [7.5, 0. ],
       [7.5, 2.5]]), array([[ 7.5,  0. ],
       [ 7.5,  2.5],
       [10. ,  2.5]]), array([[ 7.5,  0. ],
       [10. ,  0. ],
       [10. ,  2.5]]), array([[0. , 2.5],
       [0. , 5. ],
       [2.5, 5. ]]), array([[0. , 2.5],
       [2.5, 2.5],
       [2.5, 5. ]]), array([[2.5, 2.5],
       [2.5, 5. ],
       [5. , 5. ]]), array([[2.5, 2.5],
       [5. , 2.5],
       [5. , 5. ]]), array([[5. , 2.5],
       [5. , 5. ],
       [7.5, 5. ]]), array([[5. , 2.5],
       [7.5, 2.5],
       [7.5, 5. ]]), array([[ 7.5,  2.5],
       [ 7.5,  5. ],
       [10. ,  5. ]]), array([[ 7.5,  2.5],
       [10. ,  2.5],
       [10. ,  5. ]]), array([[0. , 5. ],
       [0. , 7.5],
       [2.5, 7.5]]), array([[0. , 5. ],
       [2.5, 5. ],
       [2.5, 7.5]]), array([[2.5, 5. ],
       [2.5, 7.5],
       [5. , 7.5]]), array([[2.5, 5. ],
       [5. , 5. ],
       [5. , 7.5]]), array([[5. , 5. ],
       [5. , 7.5],
       [7.5, 7.5]]), array([[5. , 5. ],
       [7.5, 5. ],
       [7.5, 7.5]]), array([[ 7.5,  5. ],
       [ 7.5,  7.5],
       [10. ,  7.5]]), array([[ 7.5,  5. ],
       [10. ,  5. ],
       [10. ,  7.5]]), array([[ 0. ,  7.5],
       [ 0. , 10. ],
       [ 2.5, 10. ]]), array([[ 0. ,  7.5],
       [ 2.5,  7.5],
       [ 2.5, 10. ]]), array([[ 2.5,  7.5],
       [ 2.5, 10. ],
       [ 5. , 10. ]]), array([[ 2.5,  7.5],
       [ 5. ,  7.5],
       [ 5. , 10. ]]), array([[ 5. ,  7.5],
       [ 5. , 10. ],
       [ 7.5, 10. ]]), array([[ 5. ,  7.5],
       [ 7.5,  7.5],
       [ 7.5, 10. ]]), array([[ 7.5,  7.5],
       [ 7.5, 10. ],
       [10. , 10. ]]), array([[ 7.5,  7.5],
       [10. ,  7.5],
       [10. , 10. ]])]
AOS Simplices 
 [array([[  0. ,  90. ],
       [  2.5, 120. ],
       [  5. ,  90. ]]), array([[ 0. , 90. ],
       [ 2.5, 60. ],
       [ 5. , 90. ]]), array([[ 2.5, 60. ],
       [ 5. , 90. ],
       [ 7.5, 80. ]]), array([[ 2.5, 60. ],
       [ 5. , 60. ],
       [ 7.5, 80. ]]), array([[ 5. , 60. ],
       [ 7.5, 80. ],
       [10. , 75. ]]), array([[ 5. , 60. ],
       [ 7.5, 60. ],
       [10. , 75. ]]), array([[ 7.5, 60. ],
       [10. , 75. ],
       [12.5, 72. ]]), array([[ 7.5, 60. ],
       [10. , 60. ],
       [12.5, 72. ]]), array([[  2.5, 120. ],
       [  5. , 120. ],
       [  7.5, 100. ]]), array([[  2.5, 120. ],
       [  5. ,  90. ],
       [  7.5, 100. ]]), array([[  5. ,  90. ],
       [  7.5, 100. ],
       [ 10. ,  90. ]]), array([[ 5. , 90. ],
       [ 7.5, 80. ],
       [10. , 90. ]]), array([[ 7.5, 80. ],
       [10. , 90. ],
       [12.5, 84. ]]), array([[ 7.5, 80. ],
       [10. , 75. ],
       [12.5, 84. ]]), array([[10. , 75. ],
       [12.5, 84. ],
       [15. , 80. ]]), array([[10. , 75. ],
       [12.5, 72. ],
       [15. , 80. ]]), array([[  5. , 120. ],
       [  7.5, 120. ],
       [ 10. , 105. ]]), array([[  5. , 120. ],
       [  7.5, 100. ],
       [ 10. , 105. ]]), array([[  7.5, 100. ],
       [ 10. , 105. ],
       [ 12.5,  96. ]]), array([[  7.5, 100. ],
       [ 10. ,  90. ],
       [ 12.5,  96. ]]), array([[10. , 90. ],
       [12.5, 96. ],
       [15. , 90. ]]), array([[10. , 90. ],
       [12.5, 84. ],
       [15. , 90. ]]), array([[12.5    , 84.     ],
       [15.     , 90.     ],
       [17.5    , 85.71429]]), array([[12.5    , 84.     ],
       [15.     , 80.     ],
       [17.5    , 85.71429]]), array([[  7.5, 120. ],
       [ 10. , 120. ],
       [ 12.5, 108. ]]), array([[  7.5, 120. ],
       [ 10. , 105. ],
       [ 12.5, 108. ]]), array([[ 10. , 105. ],
       [ 12.5, 108. ],
       [ 15. , 100. ]]), array([[ 10. , 105. ],
       [ 12.5,  96. ],
       [ 15. , 100. ]]), array([[ 12.5    ,  96.     ],
       [ 15.     , 100.     ],
       [ 17.5    ,  94.28571]]), array([[12.5    , 96.     ],
       [15.     , 90.     ],
       [17.5    , 94.28571]]), array([[15.     , 90.     ],
       [17.5    , 94.28571],
       [20.     , 90.     ]]), array([[15.     , 90.     ],
       [17.5    , 85.71429],
       [20.     , 90.     ]])]
opyrability.points2polyhedra(AIS: ndarray, AOS: ndarray) → ndarray[source]#

Generation of connected polyhedra based on the AIS/AOS points.

This function is part of Python-based Process Operability package.

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Author: San Dinh

Parameters:

  • AIS (np.ndarray) – Array containing the points that constitutes the AIS.

  • AOS (np.ndarray) – Array containing the points that constitutes the AOS.

Returns:

  • AIS_polytope (np.ndarray) – List of input (AIS) vertices for each polytope generated, in the form of an array.

  • AOS_polytope (np.ndarray) – List of output (AOS) vertices for each polyhedra generated, in the form of an array.

Example#

Generating paired polyhedrons for the AIS/AOS generated for the shower problem example.

    from opyrability import points2polyhedra
    
    AIS_poly, AOS_poly = points2polyhedra(AIS,AOS)

    print('AIS Polyhedrons \n', AIS_poly)
    print('AOS Polyhedrons \n', AOS_poly)

AIS Polyhedrons 
 [array([[0. , 0. ],
       [0. , 2.5],
       [2.5, 0. ],
       [2.5, 2.5]]), array([[2.5, 0. ],
       [2.5, 2.5],
       [5. , 0. ],
       [5. , 2.5]]), array([[5. , 0. ],
       [5. , 2.5],
       [7.5, 0. ],
       [7.5, 2.5]]), array([[ 7.5,  0. ],
       [ 7.5,  2.5],
       [10. ,  0. ],
       [10. ,  2.5]]), array([[0. , 2.5],
       [0. , 5. ],
       [2.5, 2.5],
       [2.5, 5. ]]), array([[2.5, 2.5],
       [2.5, 5. ],
       [5. , 2.5],
       [5. , 5. ]]), array([[5. , 2.5],
       [5. , 5. ],
       [7.5, 2.5],
       [7.5, 5. ]]), array([[ 7.5,  2.5],
       [ 7.5,  5. ],
       [10. ,  2.5],
       [10. ,  5. ]]), array([[0. , 5. ],
       [0. , 7.5],
       [2.5, 5. ],
       [2.5, 7.5]]), array([[2.5, 5. ],
       [2.5, 7.5],
       [5. , 5. ],
       [5. , 7.5]]), array([[5. , 5. ],
       [5. , 7.5],
       [7.5, 5. ],
       [7.5, 7.5]]), array([[ 7.5,  5. ],
       [ 7.5,  7.5],
       [10. ,  5. ],
       [10. ,  7.5]]), array([[ 0. ,  7.5],
       [ 0. , 10. ],
       [ 2.5,  7.5],
       [ 2.5, 10. ]]), array([[ 2.5,  7.5],
       [ 2.5, 10. ],
       [ 5. ,  7.5],
       [ 5. , 10. ]]), array([[ 5. ,  7.5],
       [ 5. , 10. ],
       [ 7.5,  7.5],
       [ 7.5, 10. ]]), array([[ 7.5,  7.5],
       [ 7.5, 10. ],
       [10. ,  7.5],
       [10. , 10. ]])]
AOS Polyhedrons 
 [array([[  0. ,  90. ],
       [  2.5,  60. ],
       [  2.5, 120. ],
       [  5. ,  90. ]]), array([[ 2.5, 60. ],
       [ 5. , 60. ],
       [ 5. , 90. ],
       [ 7.5, 80. ]]), array([[ 5. , 60. ],
       [ 7.5, 60. ],
       [ 7.5, 80. ],
       [10. , 75. ]]), array([[ 7.5, 60. ],
       [10. , 60. ],
       [10. , 75. ],
       [12.5, 72. ]]), array([[  2.5, 120. ],
       [  5. ,  90. ],
       [  5. , 120. ],
       [  7.5, 100. ]]), array([[  5. ,  90. ],
       [  7.5,  80. ],
       [  7.5, 100. ],
       [ 10. ,  90. ]]), array([[ 7.5, 80. ],
       [10. , 75. ],
       [10. , 90. ],
       [12.5, 84. ]]), array([[10. , 75. ],
       [12.5, 72. ],
       [12.5, 84. ],
       [15. , 80. ]]), array([[  5. , 120. ],
       [  7.5, 100. ],
       [  7.5, 120. ],
       [ 10. , 105. ]]), array([[  7.5, 100. ],
       [ 10. ,  90. ],
       [ 10. , 105. ],
       [ 12.5,  96. ]]), array([[10. , 90. ],
       [12.5, 84. ],
       [12.5, 96. ],
       [15. , 90. ]]), array([[12.5    , 84.     ],
       [15.     , 80.     ],
       [15.     , 90.     ],
       [17.5    , 85.71429]]), array([[  7.5, 120. ],
       [ 10. , 105. ],
       [ 10. , 120. ],
       [ 12.5, 108. ]]), array([[ 10. , 105. ],
       [ 12.5,  96. ],
       [ 12.5, 108. ],
       [ 15. , 100. ]]), array([[ 12.5    ,  96.     ],
       [ 15.     ,  90.     ],
       [ 15.     , 100.     ],
       [ 17.5    ,  94.28571]]), array([[15.     , 90.     ],
       [17.5    , 85.71429],
       [17.5    , 94.28571],
       [20.     , 90.     ]])]

Polytopic manipulations (advanced and internal use)#

The functions below are fundamental for operability calculations, though typical users won’t need to directly interact with them. They play a crucial role within opyrability without requiring user intervention, but are documented here nevertheless.

opyrability.get_extreme_vertices(bounds: ndarray) → ndarray[source]#

Gets the extreme vertices of any D-dimensional hypercube. This is used to plot the DOS in 3D.

Author: Victor Alves

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Parameters:

bounds (np.ndarray) – Lower and upper bounds for the Desired Output Set (DOS).

Returns:

extreme_vertices – Extreme vertices for the DOS.

Return type:

np.ndarray

opyrability.process_overlapping_polytopes(bound_box: Polytope, overlapped_intersection: Region) → Region[source]#

Eliminate overlaps between polytopes given a bounding box and a region of potentially overlapping polytopes.

The function aims to process a set of polytopes such that the resultant polytopes within the specified bounding box do not overlap with each other.

This was initially suggested by David Vinson in his Ph.D. dissertation “A new measure of process operability for the improved steady-state design of chemical processes. Ph.D. Thesis, Lehigh University, USA, 2000.”

This has been refined by me to perform the subraction of polytopes if and only if the polytopes are indeed overlapping. This is checked by function ‘are_overlapping’. Hence, computational time is largely reduced. In addition, this avoids numerical instability in the LP that could potentially lead to unbounded solutions (infesaible).

Author: Victor Alves

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Parameters:

  • bound_box (pc.Polytope) – The bounding polytope within which all other polytopes are contained.

  • overlapped_intersection (pc.Region) – A collection of polytopes (encapsulated in a pc.Region) that may potentially overlap with each other.

Returns:

A region consisting of polytopes that are within the bounding box and do not overlap with each other.

Return type:

pc.Region

opyrability.are_overlapping(poly1, poly2)[source]#

Check if two polytopes overlap.

Author: Victor Alves

Control, Optimization and Design for Energy and Sustainability (CODES) Group - West Virginia University - 2023

Parameters:

  • poly1 (Polytope) – First polytope object.

  • poly2 (Polytope) – Second polytope object.

Returns:

True if the polytopes overlap, False otherwise.

Return type:

bool

API documentation list#

opyrability